Traslación horizontal

Traslacion Horizontal

Traslación horizontal: g(x) = f(x+k) ; g(x) = f(x-k)

En este caso estamos sumando (o restando) a la coordenada x de la función f(x) una constante k para obtener la nueva gráfica de g(x). El efecto es un desplazamiento en el eje horizontal (eje de abcisas) de la función original, quedando igual en el eje vertical (eje de ordenadas).

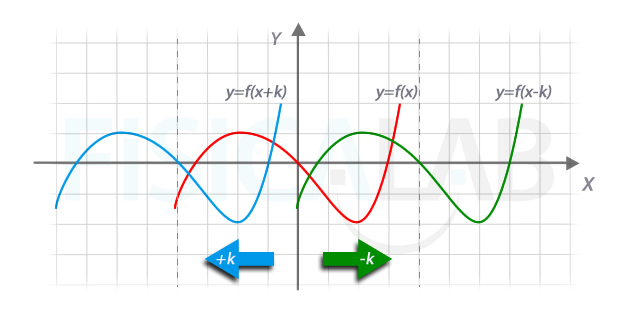
Desplazamiento horizontal

Si sumas una constante k a la variable independiente x de una función de gráfica conocida y=f(x) (en rojo) se produce un desplazamiento k unidades hacia la izquierda de la gráfica de la función original (gráfica azul). Si restas una constante k el efecto es que la gráfica de la función original se desplaza hacia la derecha k unidades (gráfica en verde).

Observa un punto cualquiera de la gráfica original. Por ejemplo, el (x,y)=(0,0). Si haces y=f(x+k), el mismo valor ypasará a estar k unidades a la izquierda, en (-k, 0). A la luz de esto, ¿sabrías decir el valor de la k de la ilustración?

Reflexión horizontal: g(x)=f(-x)

La reflexión horizontal ocurre cuando sustituimos cualquier aparición de x de una función f(x) de la que conocemos la gráfica por -x. El efecto es el de obtener la función simétrica respecto al eje y.

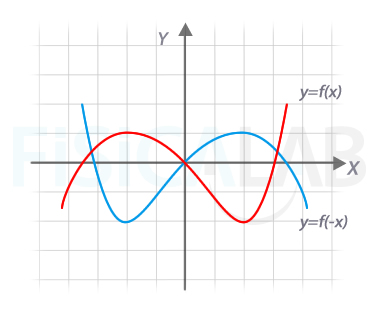
Reflexión horizontal

Dada una función, en rojo, su simétrica respecto al eje y, en azul, se obtiene cambiando x por -x en la expresión analítica de la original.

Observa un punto cualquiera de la gráfica original. Por ejemplo, el (x,y)=(-2,1). Si haces y=f(-x), el nuevo punto pasará a ser (2,1).