Transformación de Funciones Simetría
Las gráficas de las siguientes funciones f(x)=x, f(x)=x2 y f(x)=׀x׀ las conocemos. Cada una de ellas tiene una forma particular y sabemos cual es su forma general. En algunas ocasiones se nos pedirá trazar la gráfica de funciones parecidas a otras que ya conocemos. Estas se dibujan utilizando técnicas aplicadas a los modelos gráficos de cada función llamadas transformaciones. Estas transformaciones afectan la forma general de la gráfica de cada función. Las traslaciones, reflejos y las expansiones - compresiones son las transformaciones a estudiar.
Traslaciones
Las traslaciones son transformaciones que cambian la posición de la gráfica de una función. La forma general de la gráfica de una función se traslada hacia arriba, abajo, a la derecha o a la izquierda. Las traslaciones son consideradas transformaciones rígidas. Ahora veremos como se realizan estas.
Horizontal
Para obtener
la grafica de
Supóngase
que c>0
Traslación
Horizontal: Grafica
original y=f(x)
•y=g(x)=f(x-c),
se desplaza la
grafica de y=f(x) una distancia
de c unidades hacia la derecha.
•y=g(x)=f(x+c), se desplaza
la grafica de y=f(x) una distancia
de c unidades hacia la izquierda.
vertical
Supóngase
que c>0
Traslación
Vertical: Grafica
original y=f(x)
Para obtener
la grafica de
•y=g(x)=f(x)+c, se desplaza la
grafica de y=f(x) una distancia
de c unidades hacia arriba.
•y=g(x)=f(x)-c, se desplaza
la grafica de y=f(x) una distancia
de c unidades hacia abajo.
Expansiones y Compresiones
Las expansiones y compresiones son transformaciones que cambian el largo o el ancho de la gráfica de una función. La forma general de la gráfica de una función se expande o comprime verticalmente u horizontalmente. Las expansiones y compresiones son consideradas transformaciones no rígidas. Ahora veremos como se realizan estas.
Vertical
Para graficar y=af(x)
Si a>1, la gráfica de y=f(x) se expande verticalmente por un factor a. (Se alarga)
Si 0<a<1, la gráfica de y=f(x) se comprime verticalmente por un factor a. (Se encoge)
Horizontal
La gráfica de y=f(bx):
Si b>1, la gráfica de y=f(x) se comprime horizontalmente por el factor 1/b. (Se encoge)
Si 0<b<1, la gráfica de y=f(x) se expande horizontalmente por el factor de 1/b. (Se alarga)

Funciones Impar e Par
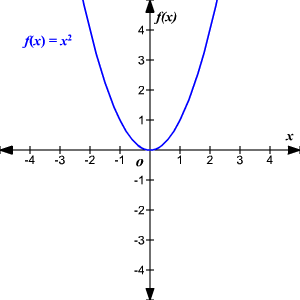
Un función es impar si, para cada x en el dominio de f , f (– x ) = – f ( x ). Las funciones impares tienen simetría rotacional de 180º con respecto del origen.
f ( x ) = x 3
f (– x ) = (– x ) 3 = – x 3 = – f ( x )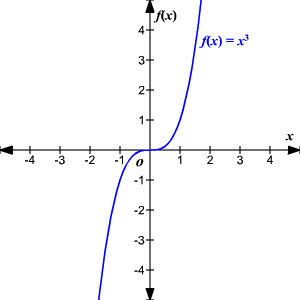




No hay comentarios:
Publicar un comentario